STL 即标准模板库(Standard Template Library),是 C++ 标准库的一部分,里面包含了一些模板化的通用的数据结构和算法。由于其模板化的特点,它能够兼容自定义的数据类型,避免大量的造轮子工作。NOI 和 ICPC 赛事都支持 STL 库的使用,因此合理利用 STL 可以避免编写无用算法,并且充分利用编译器对模板库优化提高效率。
下面对STL的一些常用用法做简单介绍,其效率可以结合其底层实现所用的算法和数据结构来理解。
STL 容器
vector-向量
使用前需include<vector>
向量(Vector)是一个封装了动态大小数组的顺序容器(Sequence Container)。跟任意其它类型容器一样,它能够存放各种类型的对象。可以简单的认为,向量是一个能够存放任意类型的动态数组。
构造函数
1 | |
2 | using namespace std; |
3 | |
4 | vector<T> vec1; // 创建一个数据类型为T的空vector vec1 |
5 | vector<T> vec2(nSize); // 创建一个数据类型为T的vector vec2,元素个数为nSize |
6 | vector<T> vec3(nSize, t); // 创建一个数据类型为T的vector vec3.元素个数为nSize, 且值均为t |
7 | vector<T> vec4(vec3); // 创建一个数据类型为T的vector vec4,并将vec3的所有元素复制到vec4中 |
8 | vector<T> vec5(vec3.begin(), vec3.end()); // 创建一个数据类型为T的vector vec5,并将vec3的所有元素复制到vec5中 |
9 | vector<T> vec6(vec3.begin() + l, vec3.begin() + r); // 将vec3的[l, r)的元素复制到vec6中 |
10 | |
11 | // 定义一个类型为T大小为 N*M 的二维动态数组 |
12 | // 方式一 |
13 | vector<vector<T> > vec7(N, vector<T>(M)); // 定义二维动态数组N行M列 |
14 | // 方式二 |
15 | vector<vector<T> > vec8(N); // 定义二维动态数组大小N行 |
16 | for(int i = 0; i < vec8.size(); i++){ // 将vec8里N个元素的每一个vector<T>类型的元素resize成长度为M |
17 | vec8[i].resize(M); |
18 | } |
19 | // 方式三 |
20 | vector<vector<T> > vec9; |
21 | vec9.resize(N); |
22 | for(int i = 0; i < N; i++) vec9[i].resize(M); |
下面是 C++ Reference 中给出的例子:
1 | // constructing vectors |
2 | |
3 | |
4 | |
5 | int main () |
6 | { |
7 | // constructors used in the same order as described above: |
8 | std::vector<int> first; // empty vector of ints |
9 | std::vector<int> second (4,100); // four ints with value 100 |
10 | std::vector<int> third (second.begin(),second.end()); // iterating through second |
11 | std::vector<int> fourth (third); // a copy of third |
12 | |
13 | // the iterator constructor can also be used to construct from arrays: |
14 | int myints[] = {16,2,77,29}; |
15 | std::vector<int> fifth (myints, myints + sizeof(myints) / sizeof(int) ); |
16 | |
17 | std::cout << "The contents of fifth are:"; |
18 | for (std::vector<int>::iterator it = fifth.begin(); it != fifth.end(); ++it) |
19 | std::cout << ' ' << *it; |
20 | std::cout << '\n'; |
21 | |
22 | return 0; |
23 | } |
其它常用函数
1 | vec.size() // 返回vec中元素的个数 |
2 | vec.empty() // 判断向量是否为空,若为空返回true,否则返回false |
3 | vec.resize(n); // 将vec的长度调整为n,若长度比当前大,则填充默认值。可利用该函数根据需要将vector调整至合适大小 |
4 | |
5 | // 增加,删除类 |
6 | vec.push_back(x); // 在vec尾部增加元素x |
7 | vec.pop_back(x); // 删除vec最后一个元素 |
8 | vec.clear(); // 清空vector |
9 | vec.insert(vec.begin() + k, x); // 在vec[k]的前面插入元素x,后面元素依次后移,与在数组中插入元素一样,效率较低 |
10 | vec.erase(vec.begin() + l); // 删除vec[l],后面元素前移,与在数组中删除元素一样,效率较低 |
11 | vec.erase(vec.begin() + l, vec.begin() + r); // 删除vec中[l, r)这段元素,后面元素前移,效率较低 |
12 | |
13 | // 遍历元素相关 |
14 | vec.begin() // 返回向量头指针,指向第一个元素 |
15 | vec.end() // 返回向量尾指针,指向向量最后一个元素的下一个位置 |
16 | vec.front() // 返回首元素的引用 |
17 | vec.back() // 返回尾元素的引用 |
18 | vec.at(k) // 返回pos位置元素的引用,一般直接像数组一样使用vec[k] |
19 | vec.rbegin() // 反向迭代器,指向最后一个元素 |
20 | vec.rend() // 反向迭代器,指向第一个元素之前的位置 |
21 | // 遍历一个vector的方式(以输出vec中所有元素为例,vec中元素为int类型) |
22 | // 方式一 |
23 | for(int i = 0; i < vec.size(); i++) printf("%d ", vec[i]); // 正向遍历 |
24 | for(int i = vec.size() - 1; i >= 0; i--) printf("%d ", vec[i]) // 反向遍历 |
25 | // 方式二 |
26 | vector<int>::iterator iter1; // 声明一个迭代器来访问vec,从而正向遍历元素 |
27 | for(iter1 = vec.begin(); iter1 != vec.end(); iter1++) printf("%d ", *iter1); |
28 | vector<int>::reverse_iterator iter2; // 声明一个反向迭代器来访问vec,从而反向遍历元素 |
29 | for(iter2 = vec.rbegin(); iter2 != vec.rend(); iter2++) printf("%d ", *iter2); |
30 | // 方式三 |
31 | for(int x: vec) printf("%d ", x); // 使用增强型for循环,遍历vec中的元素 |
stack-栈
使用前需#include<stack>
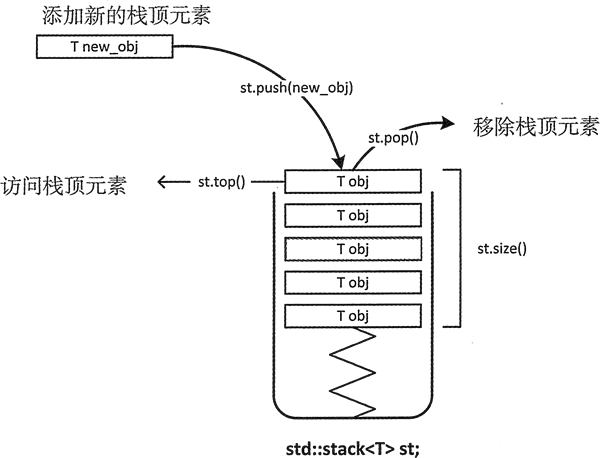
栈实现的是一种后进先出(LIFO,last-in, first-out)的策略。在栈中,只能访问 stack 顶部即最后添加的元素;只有在移除 stack 顶部的元素后,才能访问下方的元素。
1 | |
2 | using namespace std; |
3 | |
4 | stack<T> sta; // 定义一个T类型的stack容器sta |
5 | sta.push(x); // 将元素x压入sta栈顶 |
6 | sta.pop(); // 删除sta的栈顶元素 |
7 | sta.top() // 访问sta的栈顶元素 |
8 | sta.size() // 返回当前sta中的元素个数 |
9 | sta.empty() // 判断栈sta是否为空,若为空,返回true,否则返回false |
OI-wiki上的简单示例
1 | std::stack<int> s1; |
2 | s1.push(2); |
3 | s1.push(1); |
4 | std::stack<int> s2(s1); |
5 | s1.pop(); |
6 | std::cout << s1.size() << " " << s2.size() << std::endl; // 1 2 |
7 | std::cout << s1.top() << " " << s2.top() << std::endl; // 2 1 |
8 | s1.pop(); |
9 | std::cout << s1.empty() << " " << s2.empty() << std::endl; // 1 0 |
queue-队列
使用前需#include<queue>
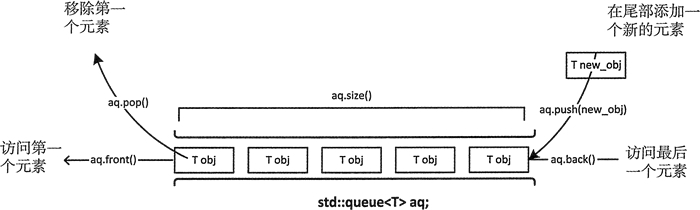
队列实现的是一个先进先出(FIFO,first-in, first-out)的策略。在队列中,只能访问第一个和最后一个元素;只能在队列的末尾(简称队尾)添加新元素,只能从队列的头部(简称队头)移除元素。
1 | |
2 | using namespace std; |
3 | |
4 | queue<T> q; // 定义一个T类型的stack容器st |
5 | q.push(x); // 在q的队尾添加一个元素x |
6 | q.pop(); // 删除q的队头元素 |
7 | q.front() // 返回q的队头元素 |
8 | q.back() // 返回q的队尾元素 |
9 | q.size() // 返回当前队列q中的元素个数 |
10 | q.empty() // 判断队列q是否为空,若为空,返回true,否则返回false |
OI-wiki上的简单示例
1 | std::queue<int> q1; |
2 | q1.push(2); |
3 | q1.push(1); |
4 | std::queue<int> q2(q1); |
5 | q1.pop(); |
6 | std::cout << q1.size() << " " << q2.size() << std::endl; // 1 2 |
7 | std::cout << q1.front() << " " << q2.front() << std::endl; // 1 2 |
8 | q1.pop(); |
9 | std::cout << q1.empty() << " " << q2.empty() << std::endl; // 1 0 |
deque-双端队列
使用前需#include<deque>
以下内容主要参考OI-wiki
std::deque是 STL 提供的 双端队列 数据结构。能够提供线性复杂度的插入和删除,以及常数复杂度的随机访问。
以下介绍常用用法,详细内容 请参见 C++ 文档。deque 的迭代器函数与 vector 相同,因此不作详细介绍。
构造函数
1 | |
2 | using namespace std; |
3 | |
4 | // 1. 定义一个int类型的空双端队列 v0 |
5 | deque<int> v0; |
6 | // 2. 定义一个int类型的双端队列 v1,并设置初始大小为10; 线性复杂度 |
7 | deque<int> v1(10); |
8 | // 3. 定义一个int类型的双端队列 v2,并初始化为10个1; 线性复杂度 |
9 | deque<int> v2(10, 1); |
10 | // 4. 复制已有的双端队列 v1; 线性复杂度 |
11 | deque<int> v3(v1); |
12 | // 5. 创建一个v2的拷贝deque v4,其内容是v4[0]至v4[2]; 线性复杂度 |
13 | deque<int> v4(v2.begin(), v2.begin() + 3); |
14 | // 6. 移动v2到新创建的deque v5,不发生拷贝; 常数复杂度; 需要 C++11 |
15 | deque<int> v5(std::move(v2)); |
元素访问
与 vector 一致,但无法访问底层内存。其高效的元素访问速度可参考实现细节部分。
at()返回容器中指定位置元素的引用,执行越界检查,常数复杂度。operator[]返回容器中指定位置元素的引用。不执行越界检查,常数复杂度。front()返回首元素的引用。back()返回末尾元素的引用。
迭代器
与 vector 一致。
长度
与 vector 一致,但是没有 reserve() 和 capacity() 函数。(仍然有 shrink_to_fit() 函数)
元素增删及修改
与 vector 一致,并额外有向队列头部增加元素的函数。
clear()清除所有元素insert()支持在某个迭代器位置插入元素、可以插入多个。复杂度与pos与两端距离较小者成线性。erase()删除某个迭代器或者区间的元素,返回最后被删除的迭代器。复杂度与insert一致。push_front()在头部插入一个元素,常数复杂度。pop_front()删除头部元素,常数复杂度。push_back()在末尾插入一个元素,常数复杂度。pop_back()删除末尾元素,常数复杂度。swap()与另一个容器进行交换,此操作是 常数复杂度 而非线性的。
deque 的实现细节(有兴趣可以了解)
deque 通常的底层实现是多个不连续的缓冲区,而缓冲区中的内存是连续的。而每个缓冲区还会记录首指针和尾指针,用来标记有效数据的区间。当一个缓冲区填满之后便会在之前或者之后分配新的缓冲区来存储更多的数据。更详细的说明可以参考 STL 源码剖析——deque 的实现原理和使用方法详解。
list-双向链表
使用前需#include<list>
以下内容主要参考OI-wiki
std::list是 STL 提供的 双向链表 数据结构。能够提供线性复杂度的随机访问,以及常数复杂度的插入和删除。
list 的使用方法与 deque 基本相同,但是增删操作和访问的复杂度不同。详细内容 请参见 C++ 文档。list 的迭代器、长度、元素增删及修改相关的函数与 deque 相同,因此不作详细介绍。
元素访问
由于 list 的实现是链表,因此它不提供随机访问的接口。若需要访问中间元素,则需要使用迭代器。
front()返回首元素的引用。back()返回末尾元素的引用。
操作
list 类型还提供了一些针对其特性实现的 STL 算法函数。由于这些算法需要 随机访问迭代器,因此 list 提供了特别的实现以便于使用。这些算法有 splice()、remove()、sort()、unique()、merge() 等。
set-集合
使用前需#include<set>
以下内容主要参考OI-wiki
set是关联容器,含有键值类型对象的已排序集,搜索、移除和插入拥有对数复杂度。set内部通常采用红黑树实现。平衡二叉树的特性使得set非常适合处理需要同时兼顾查找、插入与删除的情况。和数学中的集合相似,
set中不会出现值相同的元素。如果需要有相同元素的集合,需要使用multiset。multiset的使用方法与set的使用方法基本相同,使用前也需#include<set>。
1 | |
2 | using namespace std; |
3 | |
4 | set<T> st; // 定义一个T类型的集合st |
5 | // multiset<T> st; // 定义一个T类型的multiset st |
6 | |
7 | // 插入与删除操作 |
8 | st.insert(x); // 当容器中没有等价元素的时候,将元素x插入到st中 |
9 | st.erase(x); // 删除值为x的所有元素,返回删除元素个数(主要针对multiset,对于set而言即若st中有x则删除,否则无影响) |
10 | st.erase(pos); // 删除st中迭代器为pos的元素,要求迭代器必须合法 |
11 | st.erase(first,last); // 删除st中迭代器在 [first,last) 范围内的所有元素 |
12 | // PS: 对于multiset,若希望只删除其中一个x元素,则不能st.erase(x), 而应该st.erase(st.find(x)); |
13 | st.clear(); // 清空st |
14 | |
15 | // 迭代器 |
16 | st.begin() // 返回st指向首元素的迭代器 |
17 | st.end() // 返回st指向数组尾端占位符的迭代器,注意是没有元素的 |
18 | st.rbegin() // 返回指向逆向数组的首元素的逆向迭代器,可以理解为正向容器的末元素 |
19 | st.rend() // 返回指向逆向数组末元素后一位置的迭代器,对应容器首的前一个位置,没有元素 |
20 | |
21 | // 查找操作 |
22 | st.count(x); // 返回st内x的元素数量。(对于set即为0或1) |
23 | st.find(x); // 在st内存在键为x的元素时会返回该元素的迭代器,否则返回st.end() |
24 | st.lower_bound(x); // 返回指向首个不小于x的元素的迭代器。若不存在这样的元素,返回st.end() |
25 | st.upper_bound(x); // 返回指向首个大于x的元素的迭代器。若不存在这样的元素,返回st.end() |
26 | // 注意:不要写成 lowerbound(st.begin(), st.end(), x); 这样写也能实现效果,但是查询时间复杂度为O(n)。 |
27 | // 在set中没有自带的nth_element即查找其中第k大元素,虽然set的底层实现红黑树支持这一操作 |
28 | |
29 | st.empty() // 判断st是否为空,若为空返回true,否则返回false |
30 | st.size() // 返回容器内元素个数 |
31 | |
32 | |
33 | // set的遍历(st中元素类型为int,以输出st中所有元素为例) |
34 | // 方法一 |
35 | // 正向遍历 |
36 | set<int>::iterator iter1; // 定义一个set的迭代器 |
37 | // 正向遍历set里所有元素,这样将按照元素从小到大的顺序遍历,得到的输出升序 |
38 | for(iter1 = st.begin(); iter1 != st.end(); iter1++) printf("%d ", *iter1); |
39 | //反向遍历 |
40 | set<int>::reverse_iterator iter2; // 定义一个set的反向迭代器 |
41 | // 反向遍历set里所有元素,这样将按照元素从大到小的顺序遍历,得到的输出降序 |
42 | for(iter2 = st.rbegin(); iter2 != st.rend(); iter2++) printf("%d ", *iter2); |
43 | |
44 | // 方法二 |
45 | for(int x: st) printf("%d ", x); // 使用增强型for循环遍历set中的元素 |
set 在贪心中的使用
在贪心算法中经常会需要出现类似 找出并删除最小的大于等于某个值的元素。这种操作能轻松地通过 set 来完成。
1 | // 现存可用的元素 |
2 | set<int> available; |
3 | // 需要大于等于的值 |
4 | int x; |
5 | |
6 | // 查找最小的大于等于x的元素 |
7 | set<int>::iterator it = available.lower_bound(x); |
8 | if (it == available.end()) { |
9 | // 不存在这样的元素,则进行相应操作…… |
10 | } else { |
11 | // 找到了这样的元素,将其从现存可用元素中移除 |
12 | available.erase(it); |
13 | // 进行相应操作…… |
14 | } |
map-映射
使用需要#include<map>
以下内容主要参考OI-wiki
map是有序键值对容器,它的元素的键是唯一的。搜索、移除和插入操作拥有对数复杂度。map通常实现为红黑树。你可能需要存储一些键值对,例如存储学生姓名对应的分数:
Tom 0,Bob 100,Alan 100。但是由于数组下标只能为非负整数,所以无法用姓名作为下标来存储,这个时候最简单的办法就是使用 STL 中的map了!
map重载了operator[],可以用任意定义了operator <的类型作为下标(在map中叫做key,也就是索引)。即可以像数组一样方便地使用。
1 | |
2 | using namespace std; |
3 | |
4 | map<Key, T> yourMap; // 定义了一个键类型为Key,值类型为T的map |
5 | map<string, int> mp; // 建立一个string类型向int类型的映射 |
6 | |
7 | // 插入与删除操作 |
8 | mp["Alan"] = 100; // 可以直接通过下标访问来进行查询或插入操作 |
9 | mp.insert(pair<string,int>("Alan", 100)); // 也可通过向map中插入一个类型为pair<Key, T>的值可以达到相同目的 |
10 | mp.erase(key); // 删除mp中键为key的元素 |
11 | mp.erase(pos); // 删除mp中迭代器为pos的元素,要求迭代器必须合法 |
12 | mp.erase(first,last); // 删除迭代器在 [first,last) 范围内的所有元素 |
13 | mp.clear(); // 清空整个map |
14 | |
15 | // 查询操作 |
16 | mp.count(x); // 返回容器内键为x的元素数量(multimap不常用,所以对于map即为0或1) |
17 | // 注意:不建议通过判断 mp[x] == 0 的方式判断某个键是否存在,即使对于任意存在的键其值保证不为0 |
18 | // 因为一旦执行mp[x],如果原本mp中不存在也会增加键x,造成不必要的空间开销 |
19 | mp.find(x); // 若容器内存在键为x的元素,会返回该元素的迭代器;否则返回mp.end() |
20 | mp.lower_bound(x); // 返回mp中指向首个不小于给定键x的元素的迭代器,若不存在这样的键返回mp.end() |
21 | mp.upper_bound(x); // 返回mp中指向首个大于给定键x的元素的迭代器,若不存在这样的键返回mp.end() |
22 | |
23 | mp.empty() // 判断mp是否为空,若为空返回true,否则返回false |
24 | mp.size() // 返回容器内元素个数 |
25 | |
26 | // map的遍历(以将map<string,int> mp中的所有键值对按 key:value 的形式输出) |
27 | //方法一 |
28 | // 正向遍历 |
29 | map<string, int>::iterator iter1; |
30 | for(iter1 = mp.begin(); iter1 != mp.end(); iter1++) |
31 | cout << (*iter1).first << ":" << (*iter1).second << endl; |
32 | // 反向遍历 |
33 | map<string, int>::reverse_iterator iter2; |
34 | for(iter2 = mp.rbegin(); iter2 != mp.rend(); iter2++) |
35 | cout << (*iter2).first << ":" << (*iter2).second << endl; |
36 | |
37 | // 方法二 |
38 | for(pair<string, int> x: mp) |
39 | cout << x.first << ":" << x.second << endl; // 使用增强型for循环 |
map 用于存储复杂状态
在搜索中,我们有时需要存储一些较为复杂的状态(如坐标,无法离散化的数值,字符串等)以及与之有关的答案(如到达此状态的最小步数)。map 可以用来实现此功能。其中的键是状态,而值是与之相关的答案。下面的示例展示了如何使用 map 存储以 string 表示的状态。
1 | // 存储状态与对应的答案 |
2 | map<string, int> record; |
3 | |
4 | // 新搜索到的状态与对应答案 |
5 | string status; |
6 | int ans; |
7 | // 查找对应的状态是否出现过 |
8 | map<string, int>::iterator it = record.find(status); |
9 | if (it == record.end()) { |
10 | // 尚未搜索过该状态,将其加入状态记录中 |
11 | record[status] = ans; |
12 | // 进行相应操作…… |
13 | } else { |
14 | // 已经搜索过该状态,进行相应操作…… |
15 | } |